Grafik Fungsi Kuadrat
Di SMA sering sobat jumpai soal tentang grafik fungsi kuadrat. Biasanya pertanyaan berkutat tentang nilai ekstrem, titik puncak, bagaiman gambar grafiknya, sumbu simetri, dan lain-lain. Yang namanya grafik fungsi kuadrat adalah grafik dengan bentuk parabola (seperti gunung atau lembah). Untuk tahu bagaimana bentuk grafik dari suatu fungsi kuadrat, sobat harus memperhatikan beberapa sifat penting dari fungsi kuadrat di bawah ini.
1. Hubungan dengan sumbu y (jika x=0)
Jika dari persamaan y = ax2 + bx + c kita masukkan x = 0 maka akan ketemu y = c. Jadi titik potong parabola dengan sumbu y adalah titik dengan koordinat (0,c).
2. Hubungan dengan sumbu x (y=0)
Dari bentuk ax2 + bx + c jika y = 0 maka akan menghasilkan persamaan kuadrat ax2 + bx + c = 0, dari persamaan ini di dapat nilai D (diskriminan) D = b2-4ac.
- Jika nilai D > 0, maka parabola memotong sumbu x di dua titik yang berbeda.
- Jika nilai D = 0, maka parabola meotong sumbu x di satu titik atau bisa dikatakan parabola (grafik fungsi kuadrat) menyinggung sumbu x (titik puncak)
- Jika D < 0, maka parabola tidak memotong di sumbu x (melayang di atas atau di bawah sumbu x)
- dalam hal D < 0 dan a > 0 maka f(x) = ax2 + bx + c, akan menghasilkan nilai selalu positif (melayang di atas sumbu x)
- dalam hal D < 0 dan a < 0 maka f(x) = ax2 + bx + c, akan menghasilkan nilai selalu negatif (melayang di bawah sumbu x)
3. Harga Ekstrem dan Titik Puncak
rumus menentukan harga ekstrem
(xp,yp) = (-b/2a, D/4a)
untuk mengetahui apakah itu titik minimum atau maksimum tergantung dari nilai a. Jika a>0 maka maksimum, jika a<0 maka nilai minimum.
Titik puncak dari fungsi kuadrat f(x) = ax2 + bx + c adalah titik yang diperoleh dengan mengambil koordinat dari pasangan nilai ekstrem dengan absisnya. Koordinat puncak dari fungsi kuadrat adalah titik P (-b/2a, D/4a). Titik P dinamakan maksimum jika a > 0 dan dinamakan titik minimum jika a < 0.
4. Sumbu Simetri
Sumbu simetri merupakan garis yang ditarik dari nilai x titik ekstrem sejajar dengan sumbu y yang membelah parabola menjadi 2 bagian yang sama besar.
Persamaan untuk sumbu simetris adalah x = -b/2a
Contoh Soal Fungsi Kuadrat Dan Pembahasannya
1. Jika fungsi ) y = ax2 + 6x + (a+1) mempunyai sumbu simetri x = 3. Tentukan nilai ekstrimnya !
jawab :
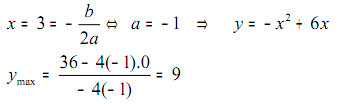
jawab :
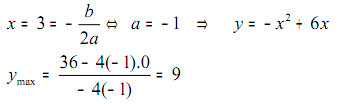
2. Jika parabola f(x) = x2-bx+7 puncaknya mempunyai absis 4, maka tentukan ordinatnya adalah?
3. Contoh soal menggambar grafik fungsi kuadrat. Jika a, b dan c bilangan real positif sembarang, maka lukislah f (x) = -ax2-bx+c


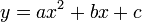
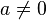
 , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
, koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.




